На плечах гигантов III. Хрустальные сферы

Читайте также:

На плечах гигантов I, или Как механика спустилась с небес на землю

На плечах гигантов II. Жрецы, кромлехи, пирамиды

От Платона до Аристотеля

Итак, древнеегипетские жрецы, они же астрономы, наблюдали и измеряли. А вот древнегреческие философы не слишком любили что-либо наблюдать, ещё меньше любили они что-нибудь измерять, а больше всего они любили изобретать всякие теории. Естественно, им больше всего хотелось придумать всеобщую теорию устройства всего на свете. Ну, понятно, нужно было как-то же заодно объяснить почему солнце восходит и заходит, с чего это луна меняет фазы, ну, и про звёзды неплохо было бы добавить… И, конечно, такая теория была придумана.

Всё началось со страшно великого древнегреческого мыслителя Платона. Он теоретически прикинул, что хорошо бы это описать движения небесных светил с помощью концентрических прозрачных сфер. Сам он не стал морочиться с такой нефилософской, с такой низменной задачей, а приказал это сделать своим ученикам.

Пожалуй, наиболее выдающимся учеником Платона был Евдокс Книдский. Он будучи, видимо, не очень типичным древним греком, каким-то образом с помощью наблюдений и расчётов вывел, что земля шарообразная и даже более-менее прикинул её диаметр. Как именно это проделал Евдокс, на сегодня неизвестно. Известен зато опыт менее древнего грека Эратосфена Киренского.

Платон. Это он подбивал астрономов городить хрустальные сферы

Евдокс Книдский

Эратосфен Киренский

Ещё древнеегипетские жрецы замечали, что в день летнего солнцестояния в Сиене (ныне Асуан) в полдень напрочь исчезают тени. Это вообще-то оттого происходит, что Асуан лежит почти строго на широте Северного Тропика. А вот в тот же самый день и тоже в полдень в Александрии, которая лежит несколько севернее, хотя и строго на том же меридиане, что и Асуан, предметы всё же отбрасывают коротенькие тени. Расстояние между городами было известно. И вот где-то за 200 лет до Рождества Христова Эратосфен измерил, под каким углом солнце отбрасывает тень в Александрии в полдень дня летнего солнцестояния. А дальше вся задача решалась чисто геометрически через подобие дуг.

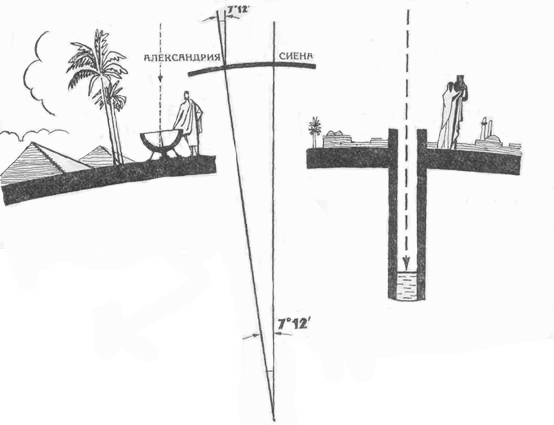
Опыт Эратосфена по измерению радиуса Земли

Вот, значит, как минимум уже 2200 лет назад кому этого хотелось, знали, что Земля никак не плоская, а вполне себе шарообразная. Это, кстати, неплохо согласовалось со стремлением учёных всех времён увидеть в этом мире высшую гармонию. Шар – фигура совершенная, без углов – красота! Эх, жаль, жаль, что не знаем мы, каким образом измерял диаметр Земли Евдокс, а ведь он делал это почти за 200 лет до Эратосфена!

И вот Евдокс по указанию Платона разработал схему движения небесных тел. Те древнейшие схемы, в число которых входит и схема Евдокса, называются гомоцентрическими (от гр. homos — общий, и centrum — центр). В таких схемах считается, что все небесные тела жёстко прикреплены к целой комбинации небесных сфер, имеющих общий центр.

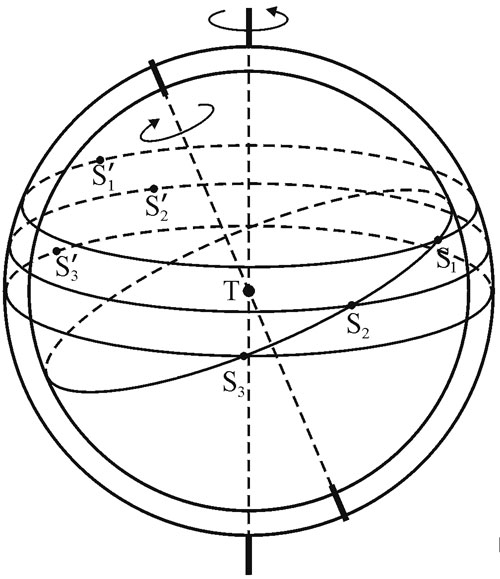
Движение Солнца в модели двух сфер (T — Земля). Внешняя сфера отвечает за суточное движение Солнца, внутренняя — за годичное

Эти схемы появились неспроста. То, что яблоки падают на землю, а не улетают за здорово живёшь в открытый космос, народ приметил вообще-то задолго до Ньютона. Архимед в своём знаменитом законе о плавании тел применял понятие веса, то есть силы, с которой тело притягивается к земле. Да и любые наблюдения показывали, что все тела стремятся упасть в сторону центра Земли. Тогда получалось, что звёзды, Солнце, Луна, планеты тоже должны рано или поздно попадать на грунт. А это было бы неприятно, потому что Солнце горячее, а Луна твёрдая. Объяснить то, что они не падают, можно было только тем, что они все приделаны к чему-то достаточно жёсткому и прочному, ну, например, к прозрачным «небесным сферам». Пре этом сферам таким твёрдым, чтобы не ломались и служили долго. Вот и гомоцентрические модели мира тоже людям служили долго…

Евдоксу для того, чтобы описать все движения луны по небосводу, понадобились три хрустальные сферы, вложенные одна в другую. Первая сфера делала оборот вокруг земли за сутки, к ней были прикреплены полюса другой сферы, которая делала оборот за 18 с половиной лет, эта сфера отражала движение точек пересечения лунной орбиты с плоскостью эклиптики*. Третья сфера крепилась внутри второй и делала оборот как раз за один лунный месяц. Три сферы пришлось присобачивать и к солнцу, для планет с их возвратными движениями этих сфер потребовалось и того больше.

Потом эту схему допиливали Каллипп и даже вроде бы сам Аристотель.

Красивые хрустальные сферы

Пифагор и «музыка сфер»

Почему «вроде бы»? Да потому что с этими древнегреческими великими философами вообще творится невероятная путаница. До Аристотеля мы ещё доберёмся, а сейчас несколько слов придётся сказать о Пифагоре.

Вот все знают теорему Пифагора про всякие там гипотенузы и катеты. И всем представляется, что Пифагор был таким себе обычным древнегреческим великим математиком, что чертил он треугольники да круги и был тем счастлив. А вот и нет. Пифагор вообще-то известен как создатель некоего мистического учения. Очень путаного, с переселением душ и всякой прочей ерундой. Но главное в его учении сводилось к тому, что он, Пифагор, самый такой умный, его приближённые, так называемые пифагорейцы, ещё туда-сюда, а остальные – дурачьё неотёсанное и он, Пифагор, должен поэтому управлять государством. Ну, прям вот всей Грецией ему поуправлять не удалось, но одной из греческих колоний в Италии он поуправлял, пока народу это не надоело, и не получил Пифагор вместе с пифагорейцами по шеям.

То есть, в основном он всё больше по политике заезжал, на математику у него, скорее всего, времени никак не оставалось. Просто так уж в те дикие времена было принято – все заслуги в любой области приписывать правителю. Изобрёл кто-нибудь айфон, а говорят, будто сам Пифагор изобрёл. Полетели стерхи на юг, так это сам Пифагор их летать научил. Вот то же и с теоремой – скорее всего её доказал кто-то из настоящих математиков в государстве Пифагора, а в газетах написали, что сам великий, мол, доказал.

Пифагор. Политик, а не математик

К чему я вообще заговорил о Пифагоре? Да вот почему. Кроме теоремы о прямоугольном треугольнике Пифагору приписывают и первые исследования в теории музыки – создание и теоретическое обоснование так называемого пифагорейского строя. Якобы никто иной, а именно сам великий и ужасный додумался, что струна, зажатая ровно посередине даёт октаву, а прижатая на 1/3 даёт чистую квинту. И вот, якобы, этот самый Пифагор придумал что, поскольку расстояния до светил и скорости их движения относятся друг к другу примерно так же как и лады на древнегреческой гитаре, хрустальные сферы при движении звучат красивыми такими аккордами. И считается, что именно от него пошло такое выражение, как «музыка сфер».

А потом ещё Платон, наслушавшись пифагорейцев, стал надоумливать своих учеников: рисуйте, мол, сферы, и всё тут! Вот и помчались бедные древнегреческие астрономы воображать красивые и музыкальные хрустальные сферы, создавая и совершенствуя гомоцентрическую модель Солнечной системы.

На гомоцентрическую модель обращали внимание даже в эпоху Возрождения, когда опять же всем с чего-то вдруг захотелось от этого мира какой-то особенной гармонии. Отметим, что красивые схемы с хрустальными сферами здорово сбивали научный люд с толку. Из-за того, что учёным мужам виделись восхитительные прозрачные сферы, сии мужи никак не могли дойти до простой, как кажется теперь, мысли, что планеты сами-то по себе – это такие сферические тела в вакууме, и что больше никаких сфер в космосе нет. И учёные старательно высчитывали как движутся планеты, приделанные к своим хрустальным сферам, и им совсем некогда было задуматься над вопросом – а почему эти самые планеты вообще движутся?

И, тем не менее, многовековые наблюдения за небом в конце концов дали результат – Ньютон нашёл ответ на вопрос «почему?» Но до этого астрономы наделали и наломали столько хрустальных сфер…

Плечи забытых гигантов

Памятник Аристарху Самосскому в Аристотелевском университете, Салоники

А ведь где-то за 300 лет до Рождества Христова ещё один умнейший древний грек Аристарх Самосский предложил даже гелиоцентрическую модель мира! Это тоже был не особенно типичный древний грек, он не особенно увлекался пустым теоретизированием, а предпочитал заниматься сперва наблюдениями и измерениями, а потом уж делать различные выводы.

Аристарх, как, впрочем, и многие другие умные древние греки и негреки, понимал, что Луна, по логике, должна быть шарообразной, как и Земля. Значит, рассуждал Аристарх, когда мы видим луну освещённой ровно наполовину, Земля, Луна и Солнце образуют прямоугольный треугольник. И если измерить угол между луной и солнцем, то можно прикинуть, насколько Солнце дальше от нас, чем Луна. Аристарх получил угол в 870, и у него вышло, что Солнце в 19 раз дальше, чем Луна. Ещё он наблюдал лунные и солнечные затмения и сообразил, что угловые размеры луны и солнца практически одинаковы. Значит, решил Аристарх, Солнце где-то раз в 20 больше, чем Луна.

Расчёты Аристарха были грубы и неточны, но это были именно научные расчёты, а не выдумывание твёрдых и хрустящих, тьфу ты, хрустальных сфер.

И вот Аристарх предположил, что Солнце-то как раз и неподвижно, а вокруг него вращаются планеты, в том числе и Земля. К несчастью сочинения Аристарха дошли до нас в виде фрагментов и упоминаний более поздних астрономов и математиков. Поэтому трудно сказать, почему Аристарх пришёл к гелиоцентрической схеме. Может быть оттого, что по его расчётам Солнце оказывалось диаметром раз в 6-7 больше Земли, и логично было предположить, что меньшее тело вращается вокруг большего. Но, скорее всего, Аристарх видел, что такая схема может хорошо описать попятное движение планет.

Однако, как мы знаем, гелиоцентрическая система «заработала» только после Ньютона. Что же мешало ей «заработать» раньше? Ведь мало того, что такая система была предложена, тем же древним грекам были известны конические сечения – гипербола, парабола, эллипс, линии, по которым и движутся вокруг Солнца планеты и другие небесные тела. Вот прям всё было в руках у этих древних греков, а они упрямо воротили хрустальные сферы, всё больше и больше сфер! В чём же дело?

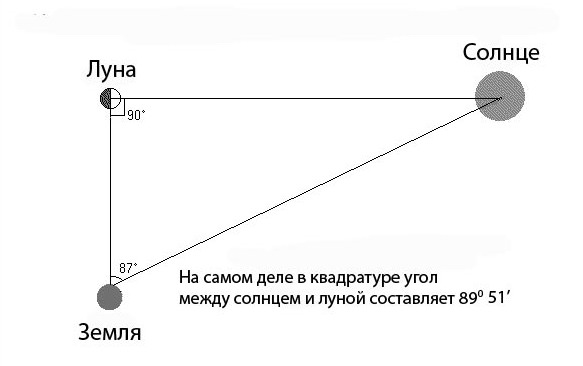
Как Аристарх Самосский определил расстояния до Солнца и Луны

Принято считать, что за такие продвинутые взгляды бедных астрономов и в античные времена подвергли бы всяческим репрессиям, как, например, некогда суд Афин приговорил Сократа к смерти по религиозным причинам. Мне же это представляется сомнительным. Сократа осудили в первую очередь по политической статье, а религию к обвинению приплели только для блезиру. Потом, если вспомнить древние языческие верования, то оказывается, что древние довольно легко меняли их, или, по крайней мере, без особого напряжения больше или меньше корректировали в зависимости от текущего момента. Конечно, так вот, щёлкнув пальчиками, перекроить религию мог только какой-нибудь древний президент, у астронома такой власти, разумеется, не было. Но не забываем, что астрономия имела в огромной степени чисто практические цели – составление точного календаря. Под хороший календарь можно было запросто и подпилить некоторые тогдашние религиозные представления. Никто бы и не поморщился.

Но в том-то и дело, что тот же Аристарх с помощью своей схемы не мог достоверно описать наблюдаемые движения небесных тел. Мало было верного предположения о гелиоцентричности, мало было и знания о конических сечениях, нужны были более точные наблюдения, которые древние греки производить не могли, нужно было умение совершать сложные математические расчёты, чего древние греки опять же не умели. И, наконец, нужно было знать законы движения, а до этого было ещё ой как далеко. И пока что более точные результаты, более соответствующие реальной картине происходящего на небе, давали хрустальные сферы. И проще было наращивать число сфер, нежели принять систему Аристарха Самосского.

И ещё, я так полагаю, сильно сказывался страх как-то поколебать авторитет великих. Вот сказал Платон, что все светила поприделаны к хрустальным сферам, значит, так оно и есть. Платон же не просто великий, он же жуть какой великий! Хотя Платон чем только не занимался, кроме реальных наблюдений и вычислений, и к астрономии с механикой не имел, ну, аж никакого отношения. Тоже всё больше теориями баловался да Атлантиды выдумывал.

Вот сказал Аристотель, что в «надлунном» мире всё движется «естественно», само по себе, значит, нечего и париться, узнавать причины движения всяких там планет, проще продолжать громоздить сферы. Хрустальные же они, чем их больше, тем лучше!

Вот сами видите, как несправедливо пишется история науки! Про Платона и Аристотеля нагородили целые тома, чуть не с первого класса школьники знают эти имена. А кто помнит Евдокса, Аристарха, Эратосфена и Гиппарха? А это всё люди, которые занимались не болтовнёй, а реальными научными исследованиями, именно благодаря ним наука всё же двигалась вперёд, медленно, преодолевая заблуждения, но двигалась. И ведь каждый из этих исследователей был действительно великим умом!

Евдокс не только построил кинематическую схему движения небесных тел, он построил первую в Греции обсерваторию, где велись систематические наблюдения за небом. Он первым в математике стал применять иррациональные числа и научился вычислять площадь криволинейных фигур.

Аристарх мало того, что самым первым предложил гелиоцентрическую модель и научно (хоть и неточно) измерил размеры Земли, Луны, Солнца и расстояния между ними, так он ещё усовершенствовал календарь, первым в вычислениях стал применять то, что сейчас называется тригонометрией, усовершенствовал солнечные часы и серьёзно занимался оптикой.

Эратосфен не только вычислил диаметр Земли с большой точностью, он также определил угловое расстояние от экватора до тропика, фундаментально занимался географией и историей, само уж собой, отметился и в математике – решил древнюю задачу об удвоении куба и изобрёл своего рода калькулятор для извлечения кубических корней.

О Гиппархе мы ещё поговорим в следующей главе, Гиппарх, можно сказать, расколотил всё это нагромождение хрустальных сфер, не оглядываясь на авторитеты Платона и Аристотеля.

А Платон и Аристотель на самом-то деле собственно наукой практически-то и не занимались, они всё больше по политике – вот, соответственно, и помнят их имена даже первоклашки. Аристотель всё больше ошивался при царском дворе, а Платон, сдружившись с пифагорейцами, всё пытался опять в той же Италии организовать «идеальное» государство. Ну-ну, знаем мы какие такие бывают идеальные государства. Раз правителю идеально, вот и государство своё он считает идеальным. А кто не согласен, то только оттого, что дурачьё. Старая песня.

А тот же Эратосфен, после того как по старости его отстранили от должности заведующего Александрийской библиотекой, умер в нищете. Вот почему некоторые современные учёные так настырно лезут в политику – открыть ничего не умеют, а прославиться им охота.

А чего ещё нагородил знаменитый Аристотель в механике, это я расскажу в следующий раз.

Продолжение следует…

Примечание:

*Эклиптика – воображаемая граница большого круга на небесной сфере вдоль которой лежит путь солнца в течение года.